
Nachdem ich im März schon die Solaranlage vormontiert hatte, …

…, dauerte das Einsetzen der Scheiben und das provisorische Einhängen dann doch bis August.

Einmal eingehängt ging der Rest innerhalb weniger Tage.

In der Abendsonne.

Nachdem ich im März schon die Solaranlage vormontiert hatte, …

…, dauerte das Einsetzen der Scheiben und das provisorische Einhängen dann doch bis August.

Einmal eingehängt ging der Rest innerhalb weniger Tage.

In der Abendsonne.
August 2010

Juli 2012


Eigentlich hätte es ja einfach sein sollen.
 War es aber nicht. Höher als breit ist noch richtig, nur die Eiform lässt mich an meinen Fähigkeiten zweifeln. Vor allem aber, mit einem schlechten Modell lässt sich keinerlei Machbarkeit belegen. Was, wenn die Zahlen falsch sind? Vermutlich habe ich nur schlampig gearbeitet. Und ich habe auch starke Vermutungen, an welchen Stellen. Nutzt nur nix! Da muss ich nochmal ran.
War es aber nicht. Höher als breit ist noch richtig, nur die Eiform lässt mich an meinen Fähigkeiten zweifeln. Vor allem aber, mit einem schlechten Modell lässt sich keinerlei Machbarkeit belegen. Was, wenn die Zahlen falsch sind? Vermutlich habe ich nur schlampig gearbeitet. Und ich habe auch starke Vermutungen, an welchen Stellen. Nutzt nur nix! Da muss ich nochmal ran.
Vorher aber brauche ich Unterstützung mathematischer Natur. Die Basislänge der langgezogenen Dreiecke, aus denen sich der Dome zusammensetzt, habe ich nur zeichnerisch ermittelt, weil ich das nicht rechnen kann. Solcherlei Geschätztes dann mit stumpfen Bleistift auf Pappe übertragen und ungenau ausgeschnitten ist für jede Sorte Fehler gut. Für den nächsten Versuch würde ich gerne wenigstens die Basislängen vor dem Kleben nachmessen können. Folgende Textaufgabe ist zu lösen:
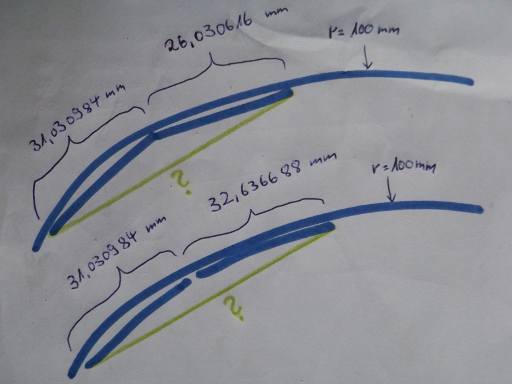 In einen Kreis mit einem gegebenen Radius sind zwei Sehnen mit gegebenen Längen einzuschreiben, so dass sie gemeinsam die Schenkel eines ungleichmäßigen Dreiecks bilden. Welche Länge hat die Basis?
In einen Kreis mit einem gegebenen Radius sind zwei Sehnen mit gegebenen Längen einzuschreiben, so dass sie gemeinsam die Schenkel eines ungleichmäßigen Dreiecks bilden. Welche Länge hat die Basis?
Aufgabe 1: r=100 mm, Sehne A=31,030984 mm, Sehne B=26,030616 mm
Aufgabe 2: r=100 mm, Sehne A=31,030984 mm, Sehne B=32,636688 mm
Könnt ihr helfen?
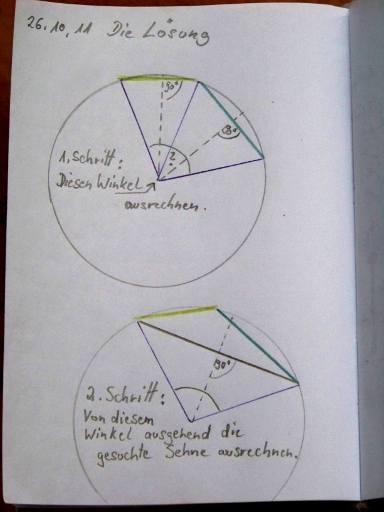
Update 26.10.2011
Das Bild zur Lösung ist zwar nicht selbsterklärend, aber es hat alles, was mir zur Lösung fehlte: die entsprechende Anzahl rechtwinkliger Dreiecke und jeweils zwei Angaben dazu.
Da hast du ein Super-Dome-Home entworfen, eigentlich fehlt nur noch ein bisschen Mathematik, und dann wird’s schwerer als gedacht. Weil, wie willst du nach etwas suchen, dessen Namen du nicht kennst. Die Wikipedia kennt eine Menge Körper (Platonische, Archimedische, Catalanische, Johnsonsche), nur genau DEN nicht. Also nochmal die Bauanleitung für einen Bambus-Dome angeschaut, die die Idee für das erste Modell geliefert hat.
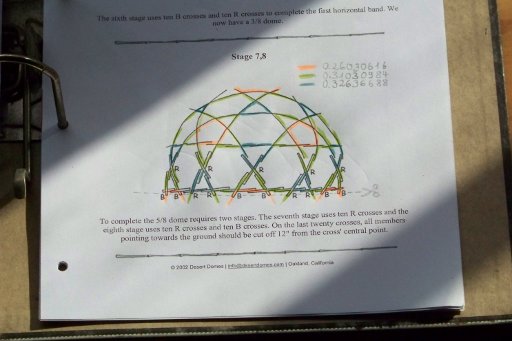 Der Bambusdome hat die gleiche geometrische Aufteilung wie dein Sechs-Fünf-Dreieck-Dings, allerdings wird er im Original aus Bambuskreuzen verschiedener Abmessungen zusammengebunden. Erst die farbliche Kennzeichnung der verschiedenen Stablängen schafft, woran scharfes Nachdenken gescheitert war, nämlich Klarheit über die Längenverhältnisse der verschiedenen Flächenkanten zueinander. Die größte Überraschung: Die Sechsecke sind nicht regelmäßig! Eigentlich hat ja alles dagestanden. Obwohl nur zwei verschiedene Bambuskreuze als Grundelemente für den Aufbau dienen, bilden diese zusammengebunden aber drei verschiedene Stablängen. Jetzt sollte es einfach werden!
Der Bambusdome hat die gleiche geometrische Aufteilung wie dein Sechs-Fünf-Dreieck-Dings, allerdings wird er im Original aus Bambuskreuzen verschiedener Abmessungen zusammengebunden. Erst die farbliche Kennzeichnung der verschiedenen Stablängen schafft, woran scharfes Nachdenken gescheitert war, nämlich Klarheit über die Längenverhältnisse der verschiedenen Flächenkanten zueinander. Die größte Überraschung: Die Sechsecke sind nicht regelmäßig! Eigentlich hat ja alles dagestanden. Obwohl nur zwei verschiedene Bambuskreuze als Grundelemente für den Aufbau dienen, bilden diese zusammengebunden aber drei verschiedene Stablängen. Jetzt sollte es einfach werden!